welcome to the world of functions! our setting- the dense jungle, the rolling fields, the deepest darkest caves, the quiet seafloor... functions are all around us in their many shapes and forms. these creatures have a quiet, powerful beauty, and i think we can work with them to make some beautiful things!

these are my familiars! i like to work with any functions, but i'm particularly attached to the deer and boars- you'll see them crop up a lot in the illustrations. i'll invite you to pick a type of function that you want to travel with now! maybe it's a bird, or a snake, or a fish, any will do! companionship on the journey always makes the walk easier :-}

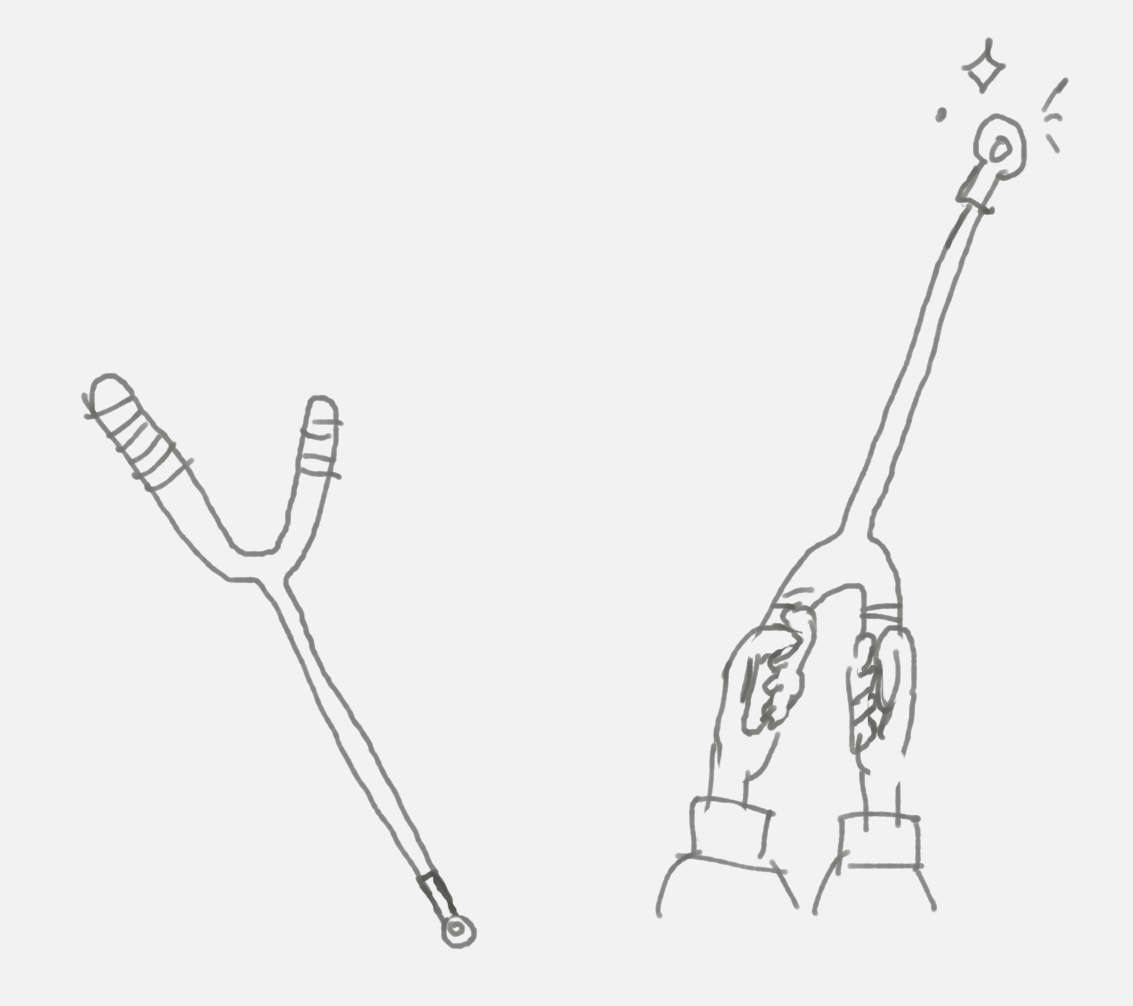
our first step to understanding functions is to be able to say where they've run off to at any given moment.. it's a bit hard to corral them at the beginning before they're used to us! to do this, we're gonna add our first tool to our caster's kit- the limit! there's newer models on the market, but i find my magiks work best when i make my tools by hand. these guy is gonna attune to any of our functions and let us track it down! there are lots of times when they'll run off to places we can't see (infinity?) or places too dangerous to go to, so this tool is indispensible.

now, how do we use it? taking a limit is really easy! for most functions, we say lim(x->a) [f(x)] is simply equal to plugging a into x. it gets a bit more complicated in other cases, though. what happens if we were to have f(x) be 1/x, and a = 0? ...yikes! that's a deep hole they've gotten themselves into! in these cases, we have to approach the problem from both sides. we know that 0 is gonna blow it up, but 0.1 should be fine! then we'll look at 0.01, 0.001 and... oh! it's getting big, fast! when we're at 0, that's definitely gonna go to infinity at this rate. from the other side, we get -inf.

for most of the cases we're using limits, that intuition should be fine. graph the function or plug in values and kind of see where it's going. i'll keep an eye out, but right now, i don't think there are any sticky limits that will require anything more than the basic limit properties (which you can look up). lhopital's rule might get the jump on us at some point though, lol. this section is kept short since there's a lot of good limits literature out there, and none of it contradicts the differential forms journey we're taking! mr paul has some great notes on them here: https://tutorial.math.lamar.edu/Classes/CalcI/LimitsIntro.aspx (with practice problems!)

so, to wrap up, why do we care about limits? well, if you don't like the * mickey mouse voice * "this tool will come in handy later!" approach, possibly appreciate that our functions are wyld beasts! these guys can get up to all sorts of trouble, and there are times when we'd like analytical ways to approach finding where their shenanigans lead them.